Answer:
The quotient of this division is
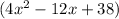 . The remainder here would be
. The remainder here would be
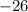 .
.
Step-by-step explanation:
The numerator
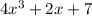 is a polynomial about
is a polynomial about
 with degree
with degree
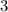 .
.
The divisor
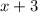 is a polynomial, also about
is a polynomial, also about
 , but with degree
, but with degree
 .
.
By the division algorithm, the quotient should be of degree
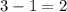 , while the remainder shall be of degree
, while the remainder shall be of degree
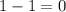 (i.e., the remainder would be a constant.) Let the quotient be
(i.e., the remainder would be a constant.) Let the quotient be
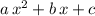 with coefficients
with coefficients
 ,
,
 , and
, and
 .
.
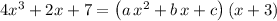 .
.
Start by finding the first coefficient of the quotient.
The degree-three term on the left-hand side is
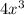 . On the right-hand side, that would be
. On the right-hand side, that would be
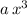 . Hence
. Hence
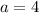 .
.
Now, given that
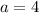 , rewrite the right-hand side:
, rewrite the right-hand side:
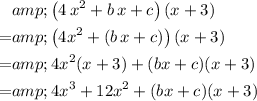 .
.
Hence:
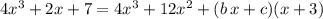
Subtract
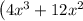 from both sides of the equation:
from both sides of the equation:
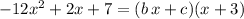 .
.
The term with a degree of two on the left-hand side has coefficient
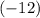 . Since the only term on the right hand side with degree two would have coefficient
. Since the only term on the right hand side with degree two would have coefficient
 ,
,
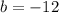 .
.
Again, rewrite the right-hand side:
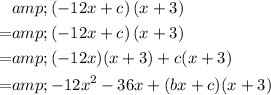 .
.
Subtract
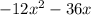 from both sides of the equation:
from both sides of the equation:
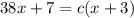 .
.
By the same logic,
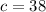 .
.
Hence the quotient would be
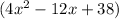 .
.