The equivalent expression is (g - f) (3) = 23
Solution:
Given that,
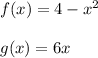
To find: (g - f)(3)
We know that,
(g - f)(x) = g(x) - f(x)
Substituting values we have:
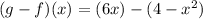
Rewriting we get,

Now let us evaluate for x = 3
Substitute x = 3 in above equation
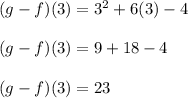
Therefore the equivalent expression is (g - f) (3) = 23