Question

In the figure, AC and BD bisect each other. Complete the statements to prove that quadrilateral ABCD is a parallelogram.

-First options:
•Alternate Interior Angles Theorem

•Vertical Angles Theorem

•Alternate Exterior Angles Theorem

-Second options:
•Converse of Alternate Exterior Angles Theorem

•Converse of Alternate Interior Angles Theorem

•Converse of Corresponding Angles Theorem

•Converse of Exterior angle theorem

Answer 1

1.B 2.B

Explanation:

Answer 2

1. Vertical Angles Theorem

2. Converse of Alternate Interior Angles Theorem

Explanation:

First option:

Lines AC and BD intersect at point E. Angles AEB and CED are opposite angles formed when these two lines intersect and are called vertical angles. By vertical angles theorem, these angles are congruent. So,

Vertical Angles Theorem

Second option:

`\triangle BEC\cong \triangle DEA` by SAS postulate, then

`\angle CBE\cong \angle ADE` as corresponding sides of congruent triangles.

Converse of Alternate Interior Angles Theorem states that if two lines are cut by a transversal and the alternate interior angles are congruent, then the lines are parallel.

So,
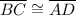`\overline{BC}\cong \overline{AD}` by

Converse of Alternate Interior Angles Theorem