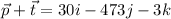Answer:
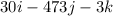
Explanation:
We are given two velocity vectors with its three components in unit notation:
Airplane's velocity:
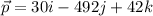
Crosswind velocity:
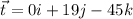
Now, if we want to know the velocity of the airplane when it is affected by the wind, we have to add these two velocity vectors:
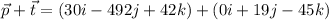
Adding both vectors: