Question

A 2x2 square is centered on the origin. It is dilated by a factor of 3. What are the coordinated of the vertices of the square? What is the ratio of the areas from the larger square to the smaller square?

Answer 1

The vertices are:

A' = (-3, -3)

B' = (3, -3)

C' = (3, 3)

D' = (-3, 3)

The ratio of area of larger square to smaller square is 9:1

Explanation:

Given:

A 2 x 2 square is centered at the origin.

So, the center of the square is (0, 0)

Since it is 2 x 2 square, the side of the square is 2 units.

So, the vertices of the 2 x 2 square are A (-1, -1), B(1, -1), C(1. 1), D(-1, 1)

The above square is dilated by a factor of 3.

Let's name the dilated square A'B'C'D'

To find the coordinates of the vertices of dilated square, we need to multiply each vertices of ABCD by 3.

A(-1, -1) = 3(-1, -1) = A'(-3, -3)

B(1, -1) = 3(1, -1) = B'(3, -3)

C(1, 1) = 3(1, 1) = C'(3, 3)

D(-1, 1) = 3(-1, 1) = D'(-3, 3)

To find the area of the small square

the side of the small square is 2 units

so the are of the small square is
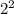`2^2` = 4 square units

To find the area of the larger square

lets find the side AB of the square using distance formula

=>
`√((x_2 -x_1)^2 +(y_2-y_1)^2)`

=>
`√((3 - (-3))^2 +(-3 - (-3))^2)`

=>
`√((3 +3)^2 +(-3 +3)^2)`

=>
`√((6)^2 +(0)^2)`

=>
`√(36)`

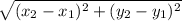
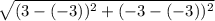
=>6

AB =6 units

In a square all the sides will be equal

Now the area of the larger square will be

`6^2`

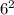
36 square units

The ratio of larger square to smaller square is

=>36 : 4

=>9 : 1