Question

Plz hurry!!!! thank you!!!!

Answer 1

Area of trapezium = 4.4132 R²

Explanation:

Given, MNPK is a trapezoid

MN = PK and ∠NMK = 65°

OT = R.

⇒ ∠PKM = 65° and also ∠MNP = ∠KPN = x (say).

Now, sum of interior angles in a quadrilateral of 4 sides = 360°.

⇒ x + x + 65° + 65° = 360°

⇒ x = 115°.

Here, NS is a tangent to the circle and ∠NSO = 90°

consider triangle NOS;

line joining O and N bisects the angle ∠MNP

⇒ ∠ONS =
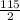`(115)/(2)` = 57.5°

Now, tan(57.5°) =
`(OS)/(SN)`

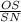
⇒ 1.5697 =
`(R)/(SN)`

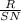
⇒ SN = 0.637 R

⇒ NP = 2×SN = 2× 0.637 R = 1.274 R

Now, draw a line parallel to ST from N to line MK

let the intersection point be Q.

⇒ NQ = 2R

Consider triangle NQM,

tan(∠NMQ) =
`(NQ)/(QM)`

⇒ tan65° =
`(NQ)/(QM)`

⇒ QM =
`(2R)/(2.1445)`

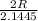
QM = 0.9326 R .

⇒ MT = MQ + QT

= 0.9326 R + 0.637 R (as QT = SN)

⇒ MT = 1.5696 R

⇒ MK = 2×MT = 2×1.5696 R = 3.1392 R

Now, area of trapezium is (sum of parallel sides/ 2)×(distance between them).

⇒ A = (
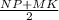`(NP + MK)/(2)`) × (ST)

= (
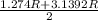`(1.274 R + 3.1392 R)/(2)`) × 2 R

= 4.4132 R²

⇒ Area of trapezium = 4.4132 R²