Question

What is angle B.........

Answer 1

I believe it’s a 30 degree angle

Answer 2

64.62°

Explanation:

Use good 'ol SOHCAHTOA. Since we know the hypotenuse and the adjacent values, we use cosine.

Therefore:

`cos( ?) = (3)/(7)`

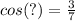
Take the inverse cosine of each side:

`{cos}^( - 1) (cos( ?)) = {cos}^( - 1) ( (3)/(7) )`

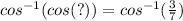
Inverse cosine of cosine cancel each other out:

`? = {cos}^( - 1) ( (3)/(7) )`

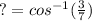
Use a calculator:

`? = 64.623`

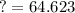
Therefore the angle is 64.62°