Answer:
The sixteenth term is
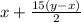 .
.
Explanation:
Given,

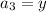
And also given,
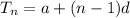
We have to find out the 16th term of given A.P.
Firstly, we will find out the common difference(d).
Common difference(d) is calculated by given formula.
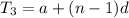
On putting the values, we get;
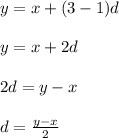
Now the value of 'd' is calculated, so we can find out the 16th term by using the formula.
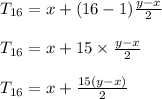
Hence The sixteenth term is
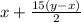 .
.