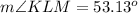Question

Plz hurry!!!! thank you!!!!

Answer 1

`m\angle KLM=53.13^o`

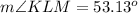
Explanation:

see the attached figure to better understand the problem

step 1

Find the measure of angle KOM

In the triangle KOM

we have

`KO=MO=r=5\ units`

`KM=8\ units`

Applying the law of cosines

`8^2=5^2+5^2-2(5)(5)cos(KOM)`

`64=50-50cos(KOM)`

`50cos(KOM)=50-64`

`50cos(KOM)=-14`

`cos(KOM)=-14/50`

`m\angle KOM=cos^(-1)(-14/50)`

`m\angle KOM=106.26^o`

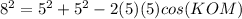
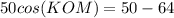
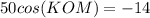
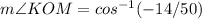
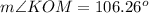
step 2

Find the measure of the arc KM

we know that

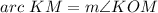`arc\ KM=m\angle KOM` ----> by central angle

we have

`m\angle KOM=106.26^o`

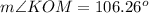
so

`arc\ KM=106.26^o`

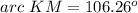
step 3

Find the measure of angle KLM

we know that

The inscribed angle is half that of the arc comprising

`m\angle KLM=(1)/(2)[arc\ KM]`

we have

`arc\ KM=106.26^o`

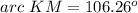
substitute

`m\angle KLM=(1)/(2)[106.26^o]`

`m\angle KLM=53.13^o`