Question is Incomplete, Complete question is given below.
Prove that a triangle with the sides (a − 1) cm, 2√a cm and (a + 1) cm is a right angled triangle.
Answer:
∆ABC is right angled triangle with right angle at B.
Explanation:
Given : Triangle having sides (a - 1) cm, 2√a and (a + 1) cm.
We need to prove that triangle is the right angled triangle.
Let the triangle be denoted by Δ ABC with side as;
AB = (a - 1) cm
BC = (2√ a) cm
CA = (a + 1) cm
Hence,
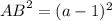
Now We know that

So;
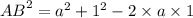
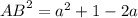
Now;
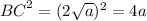
Also;
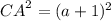
Now We know that
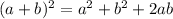
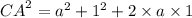
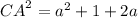

[By Pythagoras theorem]
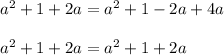
Hence,

Now In right angled triangle the sum of square of two sides of triangle is equal to square of the third side.
This proves that ∆ABC is right angled triangle with right angle at B.