Question

A farmer in China discovers a mammal hide that contains 37% of its original amount of C-14. Find the age of the mammal hide to the nearest year.

Answer 1

Answer: 54678 years

Explanation:

This can be solved by the following equation:

`N_(t)=N_(o)e^(-\lambda t)` (1)

Where:

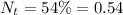`N_(t)=54\%=0.54` is the quantity of atoms of carbon-14 left after time
`t`

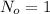`N_(o)=1` is the initial quantity of atoms of C-14 in the mammal hide

`\lambda` is the rate constant for carbon-14 radioactive decay

`t` is the time elapsed

On the other hand,
`\lambda` has a relation with the half life
`h` of the C-14, which is
`5730 years`:

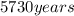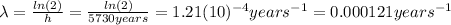`\lambda=(ln(2))/(h)=(ln(2))/(5730 years)=1.21(10)^(-4) years^(-1)=0.000121 years^(-1)` (2)

Substituting (2) in (1):

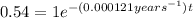`0.54=1e^{-(0.000121 years^(-1)) t}` (3)

Applying natural logarithm on both sides of the equation:

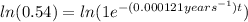`ln(0.54)=ln(1e^{-(0.000121 years^(-1)) t})` (4)

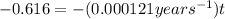`-0.616=-(0.000121 years^(-1)) t` (5)

Isolating
`t`:

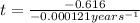`t=(-0.616)/(-0.000121 years^(-1))` (6)

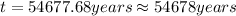`t=54677.68 years \approx 54678 years` (7) This is the age of the mammal hide