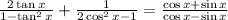 is proved
is proved
Solution:
Given that,
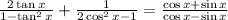
Let us first solve the L.H.S
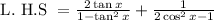 --- (1)
--- (1)
By trignometric identities,
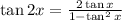
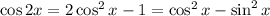
By using these in (1) we get,
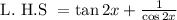
By definition of tan,
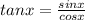
Therefore,
 --- (ii)
--- (ii)
By trignometric identities,
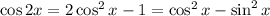
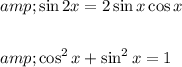
By using these in (ii)
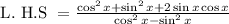 ----- (iii)
----- (iii)
We know that,
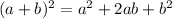
Similarly,
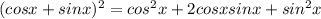
Also,
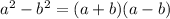
Similarly,
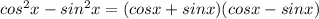
Therefore apply these in (iii)
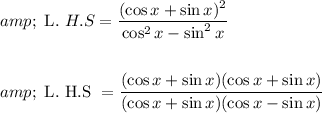
Cancel out (cos x + sin x) on numerator and denominator
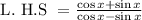
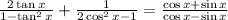
Thus L.H.S = R.H.S
Thus proved