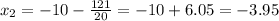Answer:
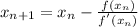
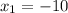

Explanation:
Generally, the Newton-Raphson method can be used to find the solutions to polynomial equations of different orders. The formula for the solution is:
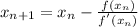
We are given that:
f(x) =
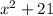 ;
;
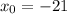
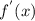 = df(x)/dx = 2x
= df(x)/dx = 2x
Therefore, using the formula for Newton-Raphson method to determine
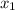 and
and
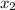
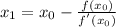
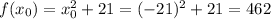
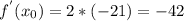
Therefore:
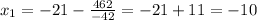
Similarly,
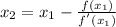
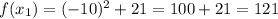
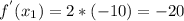
Therefore: