Answer:
a.
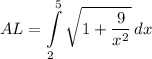
b.
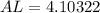
General Formulas and Concepts:
Calculus
Differentiation
- Derivatives
- Derivative Notation
Derivative Property [Multiplied Constant]:
![\displaystyle (d)/(dx) [cf(x)] = c \cdot f'(x)](https://img.qammunity.org/2021/formulas/mathematics/college/bz16ipe6p14y3f6abzxt2zy0j41tg530u9.png)
Integration
- Integrals
- Definite Integrals
- Integration Constant C
Integration Property [Multiplied Constant]:
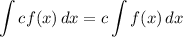
Integration Property [Addition/Subtraction]:
![\displaystyle \int {[f(x) \pm g(x)]} \, dx = \int {f(x)} \, dx \pm \int {g(x)} \, dx](https://img.qammunity.org/2021/formulas/mathematics/college/ytcjdhza3nvop8ti8icbfc977nz2k5ug6b.png)
U-Substitution
Arc Length Formula [Rectangular]:
![\displaystyle AL = \int\limits^b_a {√(1+ [f'(x)]^2)} \, dx](https://img.qammunity.org/2021/formulas/mathematics/college/jy75nc1y4bm1hn9sevbq4ns6anja5xkcvf.png)
Explanation:
Step 1: Define
Identify
y = 3ln(x)
Interval [2, 5]
Step 2: Find Arc Length
- [Function] Differentiate [Logarithmic Differentiation]:
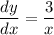
- Substitute in variables [Arc Length Formula - Rectangular]:
![\displaystyle AL = \int\limits^5_2 {\sqrt{1+ [(3)/(x)]^2}} \, dx](https://img.qammunity.org/2021/formulas/mathematics/college/v7v48aemv6ioprliwpwhl9gpiexgt0mhhu.png)
- [Integrand] Simplify:
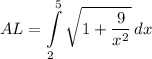
- [Integral] Evaluate:
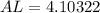
Topic: AP Calculus AB/BC (Calculus I/I + II)
Unit: Applications of Integration
Book: College Calculus 10e