Question

At the end of the day, February 14th, a florist had 120 roses left in his shop, all of which were red, white or pink in color and either long or short-stemmed. A third of the roses were short-stemmed, 20 of which were white and 15 of which were pink. The percentage of pink roses that were short-stemmed equaled the percentage of red roses that were short-stemmed. If none of the long-stemmed roses were white, what percentage of the long-stemmed roses were red?

Answer 1

25%.

Explanation:

We have been given that at the end of the day, February 14th, a florist had 120 roses left in his shop, all of which were red, white or pink in color and either long or short-stemmed.

We are also told that 1/3 of the roses were short-stemmed.

`\text{Short-stemmed roses}=120* (1)/(3)=40`

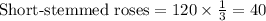
Since 20 of those were white and 15 of which were pink, so short stemmed red roses would be
`40-(20+15)=40-35=5`.

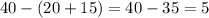Now, we will find number of long-stemmed roses by subtracting number of short-stemmed roses from total roses as:

`\text{Long-stemmed roses}=120-40=80`

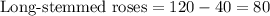
We are also told that none of the long-stemmed roses were white, so total number of white roses would be
`20+0=20`.

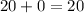Let p represent the number of total pink roses.

Now, total number of red roses would be total roses (120) minus total pink roses (p) minus total white roses (20).

`\text{Total red roses}=120-p-20`

`\text{Total red roses}=100-p`

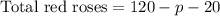
We have been given that the percentage of pink roses that were short-stemmed equaled the percentage of red roses that were short-stemmed. We can represent this information in an equation as:

`\frac{\text{Short-stemmed pink roses}}{\text{Total pink roses}}=\frac{\text{Short-stemmed red roses}}{\text{Total red roses}}`

`(15)/(p)=(5)/(100-p)`

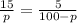
Let us solve for p by cross-multiplication:

`1500-15p=5p`

`1500-15p+15p=5p+15p`

`1500=20p`

`20p=1500`

`(20p)/(20)=(1500)/(20)`

`p=75`

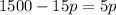
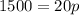
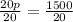
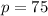
Since total number of pink roses is 75, so total number of red roses would be
`100-75=25`.

We already figured it out that 5 roses are short-stemmed, so long-stemmed roses would be
`25-5=20`.

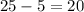Now, we have long stemmed roses is equal to 20 and total long-stemmed roses is equal to 80.

Let us find 20 is what percent of 80.

`\text{Percentage of the long-stemmed roses that were red}=(20)/(80)* 100`

`\text{Percentage of the long-stemmed roses that were red}=(1)/(4)* 100`

`\text{Percentage of the long-stemmed roses that were red}=25`

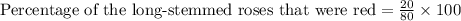
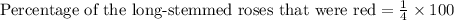
Therefore, 25% of the long-stemmed roses were red.