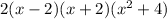Answer:
Option b) is correct.
The completed factor of given expression is
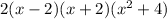
Explanation:
Given expression is
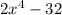
To find the completed factor for the given expression:
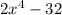 :
:
Taking the common number "2" outside to the above expression we get
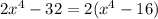
Now rewritting the above expression as below
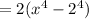 (since 16 can be written as the number 2 to the power of 4)
(since 16 can be written as the number 2 to the power of 4)
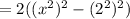
The above expression is of the form
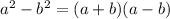
Here
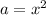 and
and
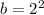
Therefore it becomes
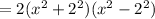
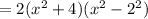
The above expression is of the form
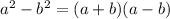
Here
 and
and
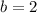
Therefore it becomes

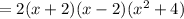
Therefore
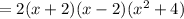
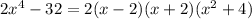
Option b) is correct.
The completed factor of given expression is