Question

Ten experts rated a newly developed chocolate chip cookie on a scale of 1 to 50. Their ratings were:

34, 35, 41, 28, 26, 29, 32, 36, 38, and 40.
1. What is the mean deviation of the ratings?
Select one:
a. 8.00
b. 4.12
c. 12.67
d. 0.75

Answer 1

b. 4.12

Explanation:

We have been given that 10 experts rated a newly developed chocolate chip cookie on a scale of 1 to 50. Their ratings were:

34, 35, 41, 28, 26, 29, 32, 36, 38, and 40.

First of all, we will find the mean of the ratings.

`\text{Mean of ratings}=(34+35+41+28+26+29+32+36+38+40)/(10)`

`\text{Mean of ratings}=(339)/(10)`

`\text{Mean of ratings}=33.9`

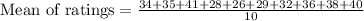
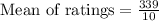
Let us find absolute deviation of each point from mean.

`|34-33.9|=0.1`

`|35-33.9|=1.1`

`|41-33.9|=7.1`

`|28-33.9|=5.9`

`|26-33.9|=7.9`

`|29-33.9|=4.9`

`|32-33.9|=1.9`

`|36-33.9|=2.1`

`|38-33.9|=4.1`

`|40-33.9|=6.1`

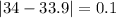
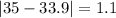
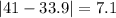
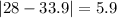
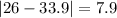
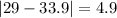
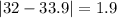
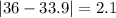
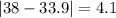
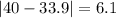
Now we will use mean deviation formula.

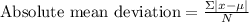`\text{Absolute mean deviation}=(\Sigma |x-\mu|)/(N)`, where,

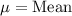`\mu=\text{Mean}` and N = Number of data points.

`MD=(0.1+1.1+7.1+5.9+7.9+4.9+1.9+2.1+4.1+6.1)/(10)`

`MD=(41.2)/(10)`

`MD=4.12`

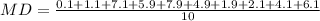
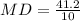
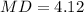
Therefore, the mean deviation of the ratings is 4.12 and option 'b' is the correct choice.

Answer 2

Option B.

Explanation:

The given data set is

34, 35, 41, 28, 26, 29, 32, 36, 38, 40

We need to find the mean deviation of the given data.

Number of observations, n = 10

Mean of the data is

`Mean=(\sum x)/(n)`

`Mean=(34+35+41+28+26+29+32+36+38+40)/(10)`

`Mean=(339)/(10)`

`Mean=33.9`

Formula for mean deviation is

`\text{Mean deviation}=(\sum |x-mean|)/(n)`

`\sum |x-mean|=|34-33.9|+|35-33.9|+|41-33.9|+|28-33.9|+|26-33.9|+|29-33.9|+ |32-33.9|+|36-33.9|+|38-33.9|+|40-33.9|=41.2`

`\text{Mean deviation}=(41.2)/(10)`

`\text{Mean deviation}=4.12`

The mean deviation of the ratings is 4.12.

Therefore, the correct option is B.