Answer:
The time = 6.5 seconds and the maximum height reached by the rocket = 676 feet
Explanation:
A path of a toy rocket thrown upward from the ground at a rate of 208 ft/sec is modeled by the quadratic function h(t) = -16
 +208t.
+208t.
We have to find when the rocket will reach its maximum height.
When the rocket reaches its maximum height,
 = 0.
= 0.
h(t) = -16
 +208t
+208t
 = - 32t + 208 = 0
= - 32t + 208 = 0
t = 6.5 seconds
At t = 6.5 seconds it is at maximum height.
Maximum height = - 16
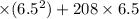
= 676 feet