Answer: b. (.54, .71)
Explanation:
Confidence interval for population proportion is given by :-
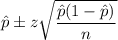
,where
 = sample proportion
= sample proportion
z= Critical z-value
n= sample size.
Let p be the proportion of people who support additional handgun control.
As per given , we have
n= 80
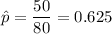
Critical z-value for 90% confidence interval is 1.645
Now , a 90% confidence interval for the population proportion of those who support additional handgun control will become:
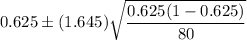
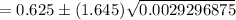

So the correct answer is : b. (.54, .71)