Answer:
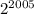
Explanation:
We are given
![f^([2005])(x) = \frac {1}{2}](https://img.qammunity.org/2021/formulas/mathematics/high-school/xchhe974lmv060wft06pm9yuh64b8i2ex1.png) .
.
Hence,
![f(f^([2004])(x))=(1)/(2)](https://img.qammunity.org/2021/formulas/mathematics/high-school/nox4r20ojyd8aavoh2acoh503ejpnxzm3z.png) .
.
Assume
![y=f^([2004])(x)](https://img.qammunity.org/2021/formulas/mathematics/high-school/3vzsnk0uyogwgb5e9pfbmrotapuq9z8zwo.png) .
.
Hence,
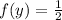 or
or
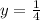 or
or
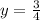 .
.
So we can conclude that
![f^([2004])(x)=(1)/(4)](https://img.qammunity.org/2021/formulas/mathematics/high-school/dq393hbn6xabp14dna5wzbsnpyihw9kk9s.png) or
or
![f^([2004])(x)=(3)/(4)](https://img.qammunity.org/2021/formulas/mathematics/high-school/ow9i2mn3oanie498vluoecfyqzrvoxi1da.png) .
.
So we can find
![f(f^([2003])(x))=(1)/(4)](https://img.qammunity.org/2021/formulas/mathematics/high-school/unsi3nhuj2rkkzykee7y99zht1s8iotdgh.png) orf(f^{[2003]}(x))=\frac{3}{4}.
orf(f^{[2003]}(x))=\frac{3}{4}.
Assume
![z=f^([2003])(x)](https://img.qammunity.org/2021/formulas/mathematics/high-school/ws5hyztw3yva39ywcnhob45gh1qb9flo5v.png) .
.
Hence,
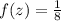 or f(z)=\frac{7}{8} or f(z)=\frac{5}{8} or f(z)=\frac{3}{8}.
or f(z)=\frac{7}{8} or f(z)=\frac{5}{8} or f(z)=\frac{3}{8}.
Therefore, we double the number of possible solutions for each iteration.
Thus, the number of solutions is
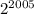 .
.