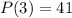Question

Use synthetic division and the remainder theorem to find P ( a).
P(x)= x^3+2 x^2-3x+5, a=3

Answer 1

For given polynomial
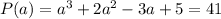`P(a)=a^3+2a^2-3a+5=41` and when a=3 is

`P(3)=41`

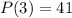
Explanation:

Given polynomial is
`P(x)=x^3+2x^2-3x+5`

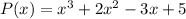
Remainder Theorem:

To evaluate the function f(x) for a given number "a" you can divide that function by x - a and your remainder will be equal to f(a). Note that the remainder theorem only works when a function is divided by a linear polynomial, which is of the form x + number or x - number.

By using synthetic division for given polynomial
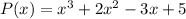`P(x)=x^3+2x^2-3x+5` and factor is (x-a) (here x-3 is a factor given)

_3| 1 2 -3 5

0 3 15 36

___________________

1 5 12 | 41

Given polynomial can be written as

`P(a)=a^3+2a^2-3a+5`

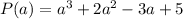
To find P(a):

`P(a)=a^3+2a^2-3a+5`

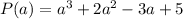
put a=3

`P(3)=3^3+2(3)^2-3(3)+5`

`P(3)=27+18-9+5`

`P(3)=41`

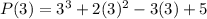
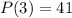
Therefore for given polynomial
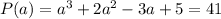`P(a)=a^3+2a^2-3a+5=41` when a=3 is
`P(3)=41`