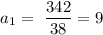Question

1) The sum of a sequence of consecutive integers is 342. The largest integer in the sequence is 3 times greater than the smallest integer in the sequence. What is the smallest integer and how many integers are in the sequence?

Due tmr tysm

Answer 1

The smallest integer is 9 and there are 19 terms in the sequence.

Explanation:

Arithmetic Sequence

The general term of an arithmetic sequence is

`\displaystyle a_n=a_1+(n-1)r\ ........[eq\ 1]`

And the sum of all n terms is

`\displaystyle s_n=(a_1+a_n)/(2)n...... [eq\ 2]`

The sequence of the question complies with

`\displaystyle s_n=342`

`\displaystyle a_n=3a_1`

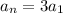
Using the last condition in eq 1 and knowing that r=1 (consecutive numbers)

`\displaystyle a_n=a_1+n-1=3a_1`

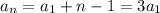
Rearranging

`\displaystyle 2a_1=n-1`

Using eq 2

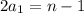
`\displaystyle (a_1+a_n)/(2)n=342`

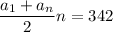
Replacing the first condition

`\displaystyle (a_1+3a_1)/(2)n=342`

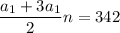
Simplifying

`\displaystyle 2a_1\ n=342`

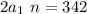
Since

`\displaystyle 2a_1=n-1`

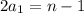
We have

`\displaystyle n(n-1)=342`

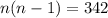
Factoring

`\displaystyle n(n-1)=(19)(18)`

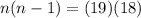
We find the number of terms

`\displaystyle n=19`

The first term is

`\displaystyle a_1=\ (342)/(38)=9`