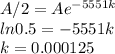Answer:
k-0.000125
Explanation:
Given that the radioactive isotope carbon-14 is present in small quantities in all life forms, and it is constantly replenished until the organism dies, after which it decays to stable carbon-12 at a rate proportional to the amount of carbon-14 present, with a half-life of 5551 years.
 , where C_1 is arbitrary constant.
, where C_1 is arbitrary constant.
Or
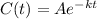
To find K.
C(t) = 1/2 C when t = 5551
i.e. A will become A/2 in 5551 years