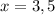Answer:
Part 1)
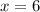
Part 2)
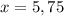
Part 3)
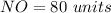
Part 4)
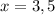
Explanation:
Part 1) Find the value of x
we know that
In a parallelogram opposites sides are congruent and parallel
In this problem
GH=FE
substitute the given values
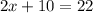
solve for x
subtract 10 both sides
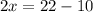
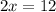
Divide by 2 both sides
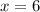
Part 2) Find the value of x
we know that
In a parallelogram opposites sides are congruent and parallel
In this problem
FG=EH
substitute the given values
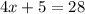
solve for x
subtract 5 both sides
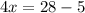
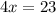
divide by 4 both sides
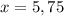
Part 3) What is the length of NO?
step 1
Find the value of x
we know that
In a parallelogram opposites sides are congruent and parallel
In this problem
NO=ML
substitute the given values
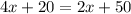
solve for x
Group terms
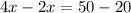
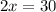
Divide by 2 both sides
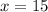
step 2
Find the value of NO
we have that
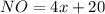
substitute the value of x

Part 4) we know that
The diagonals in a parallelogram bisect each other
so
LB=BN
LN=LB+BN ----> by addition length postulate
LN=2LB
substitute the given values
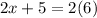
solve for x
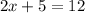
subtract 5 both sides
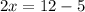
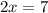
Divide by 2 both sides