Answer: The correct option is
(E) 70.
Step-by-step explanation: We are given to find the number of triangles and quadrilaterals altogether that can be formed using the vertices of a 7-sided regular polygon.
To form a triangle, we need any 3 vertices of the 7-sided regular polygon. So, the number of triangles that can be formed is

Also, to form a quadrilateral, we need any 4 vertices of the 7-sided regular polygon. So, the number of quadrilateral that can be formed is
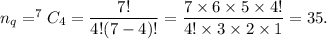
Therefore, the total number of triangles and quadrilaterals is
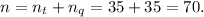
Thus, option (E) is CORRECT.