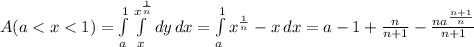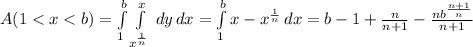Answer:
The area of the searched region is

Explanation:
If you want to find the area of a region bounded by functions f(x) and G(x) between two limits (a,b), you have to do a double integral. you must first know which of the functions is greater than the other for the entire domain.
In this case, for 0<x<1, f(x)<g(x)
while for 1<x, g(x)<f(x).
Therefore if our domain is all real numbers superior to 0 (where the limit 0<a<1 and 1<b), we have to do 2 integrals:
A=A(a<x<1)+A(1<x<b)