Answer:The type of the problem described above is a Sinking Fund
Option B
Explanation:
In order to understand the solution to this question we have to be familiar with these concepts
Sinking Fund
A sinking fund is an account earning compound interest into which you make periodic deposits. Suppose that the account has an annual interest rate of (r) compounded (m) times per year, so that (i=r/m) is the interest rate per compounding period. If you make a payment of PMT at the end of each period, then the future value after (t) years, or (n = mt) periods, will be
FV =
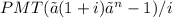
Where FV is the amount that would be accumulated after t years
Payment Formula for a Sinking Fund
Suppose that an account has an annual rate of (r) compounded (m) times per year, so that is (i=r/m) is the interest rate per compounding period. If you want to accumulate a total of FV in the account after t years, or (n = mt) periods, by making payments of PMT at the end of each period, then each payment must be
PMT =
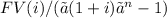
From the question
Rate= r = 3/100 = 0.03
Number of times it was paid (compounded) in a year = m = 4 its value is Four cause the payment is made 4 times in one year i.e. Quarterly
The interest rate per compounding period = I = r/m = 0.03/4 = 0.0075
Number of times it was paid (compounded) t years n = 4 x 3 = 12
The amount that ted desires to be in that account after 3 years =FV = $25,000
So the investment that Ted needs to make Quarterly in order to get his desired amount is
=
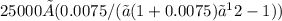
= $2000