Question

Your mathematics instructor claims that, over the years, 88% of his students have said that math is their favorite subject. In this year's class, however, only 21 out of 32 students named math as their favorite class. The instructor decides to construct a confidence interval for the true population proportion based on the sample value. What's the correct value for the standard error of pˆ in this case?

Answer 1

Answer: 0.084

Explanation:

Formula to find standard error of
`\hat{p}` for finding confidence interval for p:

`SE=\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}`

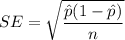
, where
`\hat{p}` = sample proportion and n= sample size.

Let p be the population proportion of students named math as their favorite class.

As per given , we have

n= 32

`\hat{p}=(21)/(32)=0.65625`

Substitute these values in the formula, we get

`SE=\sqrt{(0.65625(1-0.65625))/(32)}\\\\=√(0.00705)\\\\=0.0839642781187\approx0.084`

∴ The correct value for the standard error of
`\hat{p}` in this case = 0.084