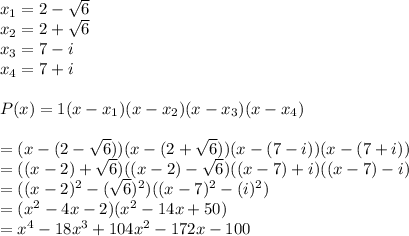Question

Find a polynomial function of least degree having only real coefficients, a leading coefficient of 1, and roots of 2-√6 , 2+ √6 , and 7-i

Answer 1

X^4-16x^3+73x^2-30x-250

Explanation:

Answer 2

`x^(4) -18x^(3)+104x^(2) -172x-100`

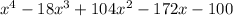
Explanation:

The 3 roots are given out of which 2 are real and 1 is imaginary. For a polynomial of least degree having real coefficients, it must have a complex conjugate root as the 4th root. Therefore, based on 4 roots, the least degree of polynomial will be 4. Finding the polynomial having leading coefficient=1 and solving it based on multiplication of 2 quadratic polynomials, we get:

`\\\\x_(1) = 2-√(6) \\x_(2) = 2+√(6) \\x_(3)=7-i \\x_(4)=7+i \\\\P(x)=1(x-x_(1))(x-x_(2) )(x-x_(3) )(x-x_(4) ) \\\\=(x-(2-√(6)))(  x-(2+√(6) )) (x-(7-i))( x-(7+i))\\=((x-2)+√(6))( ( x-2)-√(6) ) ((x-7)+i)( (x-7)-i)\\=((x-2)^(2) -(√(6) )^(2) )((x-7)^(2)-(i)^(2))\\=(x^(2) -4x-2)(x^(2) -14x+50)\\=x^(4) -18x^(3)+104x^(2) -172x-100\\`