Question

You're conducting a significance test for H0 : p = .35, Ha : p < .35. In a sample of size 40, you identify a count of 11 successes. The computed z-score and P-value are:

a. –1.06 and .1446b. –1 and .3174c. –1 and .1587d. 1 and .3174e. 1 and .8413

Answer 1

Answer: c. –1 and .1587

Explanation:

As per given , we have

Null hypothesis :
`H_0 : p= 0.35`

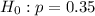
Alternative hypothesis :
`H_1 : p< 0.35`

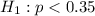
Since Alternative hypothesis is left-tailed ,so the test must be a left tailed test .

Z -Test statistic for proportion =
`z=\frac{\hat{p}-p}{\sqrt{(p(1-p))/(n)}}`

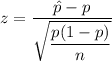
, where p= population proportion

`\hat{p}` = sample proportions

n= Sample size.

Let x be the number of successes.

For n= 40 and x= 11

`\hat{p}=(x)/(n)=(11)/(40)=0.275`

Then ,
`z=\frac{0.275-0.35}{\sqrt{(0.35(1-0.35))/(40)}}`

`z=(-0.075)/(√(0.0056875))`

`z=(-0.075)/(0.075415515645)`

`z=-0.99449031619\approx-1`

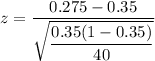
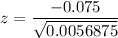
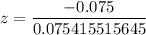
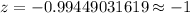
By using z-table ,

P-value for left-tailed test = P(z<-1)= 1-P(z<1) [∵ P(Z<-z)= 1-P(Z<z) ]

= 1-0.8413

=0.1587

Hence, the -score and P-value are –1 and 0.1587 .

So the correct option is c. –1 and .1587