Answer: c. –1 and .1587
Explanation:
As per given , we have
Null hypothesis :
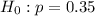
Alternative hypothesis :
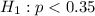
Since Alternative hypothesis is left-tailed ,so the test must be a left tailed test .
Z -Test statistic for proportion =
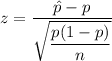
, where p= population proportion
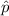 = sample proportions
= sample proportions
n= Sample size.
Let x be the number of successes.
For n= 40 and x= 11
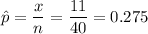
Then ,
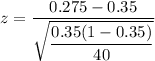
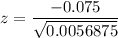
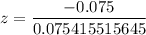
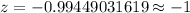
By using z-table ,
P-value for left-tailed test = P(z<-1)= 1-P(z<1) [∵ P(Z<-z)= 1-P(Z<z) ]
= 1-0.8413
=0.1587
Hence, the -score and P-value are –1 and 0.1587 .
So the correct option is c. –1 and .1587