Question

A random sample of 250 men yielded 175 who said they'd ridden a motorcycle at some time in their lives, while a similar sample of 215 women yielded only 43 that had done so. Find a 99% confidence interval for the difference between the proportions of men and women who have ridden motorcycles.

a. .5 ± .103

b. .5 ± .085

c. .5 ± .112

d. .4688 ± .085

e. .5 ± .078

Answer 1

Option a is right

Explanation:

Given that a random sample of 250 men yielded 175 who said they'd ridden a motorcycle at some time in their lives, while a similar sample of 215 women yielded only 43 that had done so.

For proportions since binomial and sample size large we can use z critical values.

Sample I II

N 250 215 465

X 175 43 218

p 0.7 0.2 0.4688

p difference = 0.5

Std error of difference =
`\sqrt{p(1-p)((1)/(n_1)+  (1)/(n_2) }\\=\sqrt{0.4688*0.5312)((1)/(250) + (1)/(215) )}\\=0.0409`

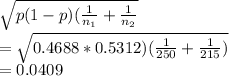
Margin of error for 99% = 2.58*std error = 0.105

Confidence interval 99% = (0.5±0.105)

Option a is right.