Question

If cos x= sin(20 + x)° and 0° < x < 90°, what is the value of x

Answer 1

If cos x= sin(20 + x)° and 0° < x < 90° then value of x is 35 degrees

Solution:

Given that:

`cos x= sin (20 + x)`

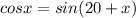
We know that,

`sin (a+b)=sin a * cos b+cos a * sin b`

`cos x= sin (20 + x) = sin 20 cos x + cos 20 sin x`

`cos x-sin20 * cos x=cos 20 * sin x`

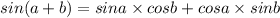
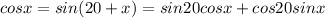
Taking cos x as common,

`cos x(1-sin 20)=cos 20 * sin x`

`((1-sin 20))/((cos 20))=(sin x)/(cos x )\\\\tan x = ((1-sin 20))/((cos 20))`

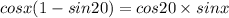
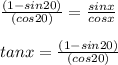
By trignometric functions,

sin 20 = 0.34202

cos 20 = 0.939692

So,

`tan x = (1 - 0.34202)/(0.939692)\\\\tan x = 0.7002`

Therefore,

x = arc tan (0.7002)

x = 35 degrees

Therefore value of x is 35 degrees

Method 2:

cos x = sin (20 + x)

sin and cos are co - functions, which means that:

cos x = cos [90 - (20 + x)]

cos x = cos (90 - 20 - x)

cos x = cos (70 - x)

Therefore, x = 70 - x

x + x = 70

2x = 70

x = 35

Therefore value of x is 35 degrees