Question

Robert's dog is 4 years older than Karen's cat. In 3 years, the sum of the ages of Robert's dog and Karen's cat will be 13. How old is Robert's dog right now?

Answer 1

5.5 years old.

Explanation:

Let D represent present age of Robert's dog and C represent present age of Karen's cat.

We have been given that Robert's dog is 4 years older than Karen's cat. We can represent this information in an equation as:

`D=C+4...(1)`

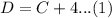
We are also told that in 3 years, the sum of the ages of Robert's dog and Karen's cat will be 13. After 3 years age of dog and cat would be
`D+3` and
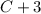`C+3` respectively.

We can represent this information in an equation as:

`D+3+C+3=13...(2)`

From equation (1), we will get:

`C=D-4`

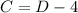
Upon substituting this value in equation (2), we will get:

`D+3+D-4+3=13`

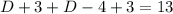
Combine like terms:

`2D+2=13`

`2D+2-2=13-2`

`2D=11`

`(2D)/(2)=(11)/(2)`

`D=5.5`

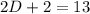
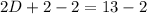
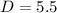
Therefore, Robert's dog is 5.5 years old right now.