Question

Find equation of set of points pieces that its distance from the point 3, 4, -5 and -2, 1, 4 are equal.

Answer 1

Explanation:

Suppose we a point
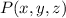`P(x,y,z)` such that its distance from either the point
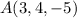`A(3,4,-5)` or
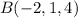`B(-2,1,4)` is the same.

Using this information we can formula:

distance AP = distance BP

first, let's find the distance from AP, using the distance formula.

`r = √((x_1 - x_2)^2 + (y_1 - y_2)^2 + (z_1 - z_2)^2)`

`AP = √((3 - x_2)^2 + (4 - y_2)^2 + (-5 - z_2)^2)`

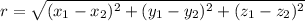
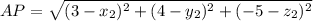
similarly, we can find the distance BP

`BP = √((-2 - x_2)^2 + (1 - y_2)^2 + (4 - z_2)^2)`

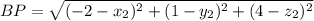
since both distances are exactly the same we can equate them

`AP = BP`

`√((3 - x_2)^2 + (4 - y_2)^2 + (-5 - z_2)^2) = √((-2 - x_2)^2 + (1 - y_2)^2 + (4 - z_2)^2)`

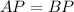
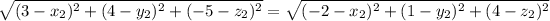
we can simplify it a bit squaring both sides, and getting rid of the subscripts.

`(3 - x)^2 + (4 - y)^2 + (-5 - z)^2 = (-2 - x)^2 + (1 - y)^2 + (4 - z)^2`

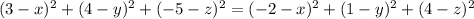
what we have done here is formulated an equation which consists of any point P that will have the same distance from (3,4,-5) and (-2,1,4).

To put it more concretely,

This is the equation of the the plane from that consists of all points (P) from which the distance from both (3,4,-5) and (-2,1,4) are equal.