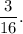Question

You have a deck of 52 cards. What’s the probability you draw exactly 1 heart in 2 draws with replacement?

Answer 1

Answer: The probability you draw exactly 1 heart in 2 draws with replacement is 3/16

Explanation:

The probability of picking a heart in a pack of 52 playing card is

13/52=1/4

The probability of drawing exactly one heart in 2 draws with replacement mean;

That the first draw is a heart and the second draw is not a heart

The probability that the second draw is not a heart is= 1-1/4= 3/4

Therefore

The probability you draw exactly 1 heart in 2 draws with replacement is

1/4 * 3/4 = 3/16

Answer 2

Answer: The required probability is
`(3)/(16).`

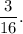
Step-by-step explanation: Given a deck of 52 cards.

We are to find the probability of drawing exactly 1 heart in 2 draws with replacement.

Number of hearts in the deck = 13.

Let S be the sample space of drawing two cards from the deck of 52 cards and E denote the event of drawing exactly 1 heart in 2 draws with replacement.

Then,

`n(S)=^(52)C_1*^(52)C_1=52*52,\\\\\\n(E)=^(13)C_1*^(52-13)C_1=13*39.`

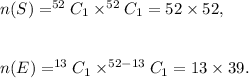
Therefore, the probability of event E is

`P(E)=(n(E))/(n(S))=(13*39)/(52*52)=(1*3)/(4*4)=(3)/(16).`

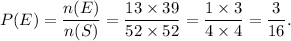
Thus, the required probability is
`(3)/(16).`