Question

Prove F is close if and only if F is a finite intersection of closed sets finite uniona) trueb) false

Answer 1

This statement is true

Explanation:

Remember that subset F of a metric (or topological) space X is said to be closed if X-F is open according to the metric (topology) of F.

Let F⊆X. For the "if" part, suppose that
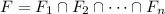`F=F_1\cap F_2\cap \cdots \cap F_n` where
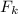`F_k` is a closed set for all k. Then by De Morgan's law,
`X-F=(X-F_1)\cup(X-F_2)\cup \cdots\cup(X-F_n)`.

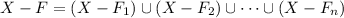Now, since Fk is closed for all k, then X-Fk is open. In every metric (topological) space, the union of an arbitrary family of open sets open sets is open, thus X-F is open, that is, F is closed.

For the "only if" implication, suppose that F is closed. We always have that F=F∩F (y∈F if and only if y∈F and y∈F if and only if y∈F∩F). then F is a finite intersection of closed sets (F and F).