Question

Suppose that $p$ and $q$ are positive numbers for which \[\log_9 p = \log_{12} q = \log_{16} (p + q).\] Then $q/p$ can be expressed in the form $(x + \sqrt{y})/z$, where $x$, $y$, and $z$ are positive integers, and $y$ is not divisible by the square of a prime. Find $x + y + z$.

Answer 1

Value of (x + y + z) = 8

Explanation:

Suppose p and q are the positive numbers for which

`log_(9)p=log_(12)q=log_(16)(p+q)`

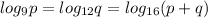
from the given expression,

`log_(9)p=log_(12)q`

`(logp)/(log9)=(log(q))/(log12)`

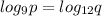
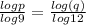
log(p).log(12) = log(q).log(9)

log(q).2log(3) = log(p).log(12) ------(1)

Now
`log_(12)q=log_(16)(p+q)`

`(logq)/(log12)=(log(p+q))/(log(16))`

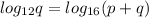
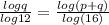
log(q).log(16) = log(p + q).log(12)

2log(4).log(q) = log(p + q).log12 -------(2)

By adding both the equations (1) and (2),

2log(3).log(q) + 2log(4).log(q) = log(12).log(p) + log(12).log(p + q)

log(q)[2log(3) + 2log(4)] = log(12)[logp + log(p + q)]

2log(q).log(12) = log(12).log[p.(p + q)]

2log(q) = log[p.(p+q)]

q² = p(p + q)

`(q)/(p)=(p+q)/(q)`

`(q)/(p)=(p)/(q)+1`

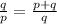
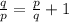
Let
`(q)/(p)=a`

a =
`(1)/(a)+1`

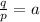
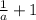
a² - a - 1 = 0

from quadratic formula,

a =
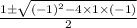
`\frac{1\pm \sqrt{(-1)^(2)-4* 1* (-1)}}{2}`

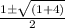
a =
`(1\pm √((1+4)))/(2)`

a =
`(1\pm √((5)))/(2)`

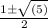
If the solution is represented by
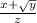`(x+√(y))/(z)` then it will be equal to

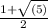`(1+√((5)))/(2)` then x = 1, y = 5 and z = 2.

Now we have to find the value of (x + y + z).

By placing the values of x, y and z,

(x + y + z) = (1 + 5 + 2) = 8

Therefore, value of (x + y + z) = 8