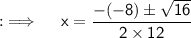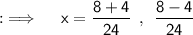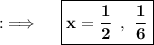Question

Find the roots of the quadratic equation
(4p - 1)² = 4p².
​

Answer 1

We are given with a quadratic equation, but before solving the equation, let's convert it to the standard form of a quadratic equation i.e ax² + bx + c = 0 first ;

`{:\implies \quad \sf (4p-1)^(2)=4p^(2)}`

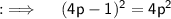
Using the identity (a - b)² = a² + b² - 2ab, we will be having

`{:\implies \quad \sf (4p)^(2)+(1)^(2)-2* 4p* 1=4p^(2)}`

`{:\implies \quad \sf 16p^(2)-8p-4p^(2)+1=0}`

`{:\implies \quad \sf 12p^(2)-8p+1=0}`

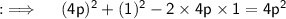
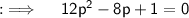
So, now if we compare it with the standard form of quadratic equation, we will be having a = 12, b = -8 and c = 1, so now Discriminant (D) = b² - 4ac = (-8)² - 4 × 12 × 1 = 64 - 48 = 16, now as D > 0, so two real and distinct roots exist, so now by quadratic formula we know that ;

• 
  `{\boxed{\bf{x=(-b\pm √(D))/(2a)}}}`

So, now solving for x, we will be having ;

`{:\implies \quad \sf x=(-(-8)\pm √(16))/(2* 12)}`

`{:\implies \quad \sf x=(8\pm 4)/(24)}`

`{:\implies \quad \sf x=(8+4)/(24)\:\:,\:\: (8-4)/(24)}`

`{:\implies \quad \sf x=(12)/(24)\:\:,\:\: (4)/(24)}`

`{:\implies \quad \boxed{\bf{x=(1)/(2)\:\:,\:\: (1)/(6)}}}`