Answer:
a)
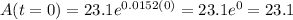
b)
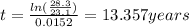
So for this case the answer would be 13.347 years, the population will be 28.3 million and ye year would be 2000+13.347 and that would be approximately in 2014
Explanation:
For this case we assume the following model:
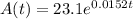
Where t is the number of years after 2000/
Part a
For this case we want the population for 2000 and on this case the value of t=0 since we have 0 years after 2000. If we rpelace into the model we got:
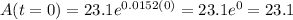
So then the initial population at year 2000 is 23.1 million of people.
Part b
For this case we want to find the time t whn the population is 28.3 million.
So we need to solve this equation:
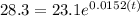
We can divide both sides by 23.1 and we got:
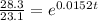
Now we can apply natural log on both sides and we got:

And then for t we got:
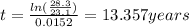
So for this case the answer would be 13.347 years, the population will be 28.3 million and ye year would be 2000+13.347 and that would be approximately in 2014