Question

The rectangle below has an area of 70y^8+30y^6.The width of the rectangle is equal to the greatest common monomial factor of 70y^8 and 30y^6. What is the length and width of the rectangle?

Answer 1

Width
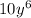`10y^6` units

Length
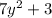`7y^2+3` units

Explanation:

The rectangle has an area of
`70y^8+30y^6.`

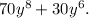
The width of the rectangle is equal to the greatest common monomial factor of
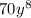`70y^8` and
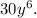`30y^6.` Find this monomial factor:

`70y^8=2\cdot 5\cdot 7\cdot y^8\\ \\30y^6=2\cdot 3\cdot 5\cdot y^6\\ \\GCF(70y^8,30y^6)=2\cdot 5\cdot y^6=10y^6`

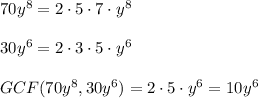
Hence, the width of the rectangle is
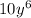`10y^6` units.

The area of the rectangle can be rewritten as

`10y^6(7y^2+3).`

The area of the rectangle is the product of its width by its length, then the length of the rectangle is
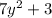`7y^2+3` units.