Question

Mike and Menna were instructed to graph the function y = 12 x + 1. Their graphs are shown.

The figure shows two graphs in the xy-plane. The graph on the left is labeled as Mike's Graph. The values on the x-axis range from negative 8 to 8 in increments of 2 and the values on the y-axis range from negative 8 to 8 in increments of 2. A line is shown which intersects the x-axis at negative 0.5 and y-axis at 1. The graph on the right is labeled as Menna's Graph. The values on the x-axis range from negative 8 to 8 in increments of 2 and the values on the y-axis range from negative 8 to 8 in increments of 2. A line is shown which intersects the x-axis at 2 and y-axis at 1.

Which student graphed the function correctly?
What mistake did the other student make?

Answer 1

Explanation:

y = 2x + 1.

Answer 2

The function is y = 2x + 1.

And mike graphed the function correctly.

Menna took the point where the function touches x-axis incorrectly.

Instead of (-1/2,0), Menna took it as (-2,0)

Explanation:

The equation y = mx +c indicates a straight line whose slope is m

And y-intercept is c.

y-intercept is nothing but the distance between origin and point where the graph crosses the y-axis (0,c).

Now, this graph crosses x-axis when y = 0.

⇒ mx + c = 0; ⇒ x =
`(-c)/(m)`.

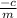Now, by comparing y = 2x + 1 with y = mx + c.

m=2 and c=1

⇒ the graph should crosses y-axis at (0,c) = (0,1)

And touch x-axis at (
`(-c)/(m)` , 0) = (
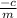`(-1)/(2)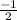`,0)

⇒ mike graphed the function correctly.

Menna took the point where the function touches x-axis incorrectly.

Instead of (-1/2,0), Menna took it as (-2,0)