Question

The curve c(t) = (cost,sint,t) lies on which of the following surfaces. Enter T or F depending on whether the statement is true or false. (You must enter T or F -- True and False will not work.)___ 1. a plane___ 2. a sphere___ 3. an ellipsoid___ 4. a circular cylinder

Answer 1

1. Plane False

2. Sphere False

3. Ellipsoid False

4. Circular cylinder True

Explanation:

For this case we have the following curve
`C(t) = (cos t , sin t , t`

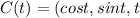
And we can express like this the terms for the curve or each component:

`x= cos t, y= sin t , z =t`

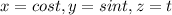
1. Plane False

The general equation for a plane is given by:

a ( x − x 1 ) + b ( y − y 1 ) + c ( z − z 1 ) = 0.

For this case we don't satisfy this since have sinusoidal functions and this equation is never satisfied.

2. Sphere False

The general equation for a sphere is given by:

(x - a)² + (y - b)² + (z - c)² = r²

And for this case if we see our parametric equation again that is not satisfied since we have two cosenoidal functions. And another function z=t

3. Ellipsoid False

The general equation for an ellipsoid is given by:

x^2/a2 + y^2/b2 + z^2/c2 = 1

And for this case again that's not satisfied since we have

`(cos^2 t)/(a^2) + (sin^2 t)/(b^2)+(t^2)/(c^2) \\eq 1`

4. Circular cylinder True

The general equation for a circular cylinder is given by:

`x^2 +y^2 = r^2`

And if we replace the equations that we have we got:

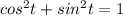`cos^2 t + sin^2 t = 1` from the fundamental trigonometry property.

So then we see that our function satisfy the condition and is the most appropiate option.