Question

Suppose p(x) is a polynomial of smallest possible degree such that: bullet p(x) has rational coefficients bullet p(-3) = p(\sqrt 7) = p(1-\sqrt 6) = 0 bullet p(-1) = 8 determine the value of p(0).

Answer 1

p(0) = 35

Explanation:

-3, √7 and 1-√6 are all roots, hence, we can factorize (x-(-3)) = (x+3), (x-√7) and (x- (1-√6)) = (x-1+√6) from p. Since p has rational coefficients, then we need to cancel out both √7 and √6. To do so we should multiply by the rational conjugate, of the expressions (x-1+√6) and (x-√7), that means, where a square root of a non square positive number appears, place the opposing sign there.

The rational conjugate of (x-√7) is (x+√7), and

(x-√7)*(x+√7) = x²-7

On the other hand, the rational conjugate of (x-1+√6) is (x-1-√6), and

(x-1+√6) * (x-1-√6) = ( (x-1) + √6) * ((x-1) -√6) = (x-1)² - √6² = x²-2x+1-6 = x²-2x-5.

Thus, both x²-7 and x²-2x-5 are factors of p. The polynomial has the form

`P(x) = c(x+3)(x^2-7)(x^2-2x-5)`

Where c is a constant. To determine c, we need to use the other piece of information given: p(-1) = 8

When we evaluate in -1, we get

`p(-1) = c*(-1+3)((-1)^2-7)((-1)^2-2(-1)-5) = c* 2*(-6)*(-2) = c*24 = 8`

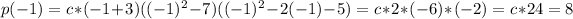
Thus, c = 8/24 = 1/3.

Therefore,

`p(0) = (1)/(3) * (0+3)(0^2-7)(0^2-2*0-5) = (1)/(3)*3*(-7)*(-5) = 35`

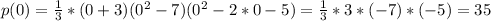
I hope that works for you!