Question

Calculate the rotational inertia of a meter stick, with mass 0.71 kg, about an axis perpendicular to the stick and located at the 18 cm mark. (Treat the stick as a thin rod.)

Answer 1

To solve this problem we will use the parallel axis theorem for which the inertia of a point of an object can be found through the mathematical relation:

`I = I_(cm) +mx^2`

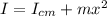
Where

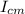`I_(cm)` = Inertia at center of mass

m = mass

x = Displacement of axis.

Our mass is given as 0.71kg,

m = 0.71kg

Para a Stick with length (L) the Moment of Inertia of the stick about and axis passing through the center and perpendicular to stick is

`I_(cm) = (1)/(12) mL^2`

`I_(cm) = (1)/(12) (0.71)(1)^2`

`I_(cm) = 0.05916Kg\cdot m^2`

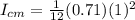
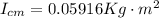
The distance between center of mass to the specific location is

`x = 50cm - 18cm`

`x = 38cm = 0.38m`

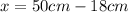
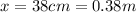
So, from parallel axis theorem ,

`I = I_(cm) + mx^2`

`I =0.05916Kg\cdot m^2+ (0.71kg)(0.38m)^2`

`I = 0.161684Kg\cdot m^2`

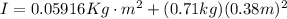
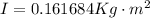
Therefore the rotational inertia is
`0.161684Kg\cdot m^2`