Answer:
The least possible value is -2, obtained for a = -1 and b = 1.
Explanation:
We want the minimum of
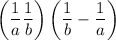 , where
, where
First, lets simplify the expression given, we use common denominator on the second part, using ab as the common denominator. We obtain
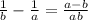
As a result
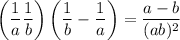
we need the minimum of the function
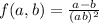
with the restrictions
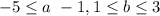
First, we calculate the gradient of f and find where it takes the zero value.
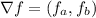
with
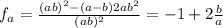
Since it has the reversed sign, we get

In order for
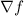 to be zero, we need both
to be zero, we need both
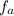 and
and
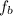 to be zero, observe that
to be zero, observe that
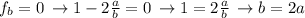
Which is impossible with the given restrictions. Hence, the minimum is realized in the border.
If we fix a value a₀ for a, with a₀ between -5 and -1 the function g(b) = f(a₀,b) wont have a minimum for b in [1,3] because the partial derivate of f over b didnt reach the value 0 in the restrictions given. On the other hand. by making a similar computation that before, we can obtain that the partial derivate of f over the variable a doesnt reach the value 0 either. This means that f doesnt reach the minimum on the sides. As a consecuence, it reach a minimum on the corners.
The 4 possible corner values are (-5,1), (-5,3), (-1,1) and (-1,3)
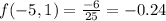
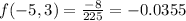
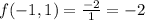
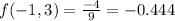
Clearly the least possible value between the four corners is -2.