Question

What are the zero(s) of the function f(x)=
`(4x^(2)-36x )/(x-9)`?

a.) x = -9
b.)x = 0
c.)x = 9
d.)x = 0 and x = 9

Answer 1

D

Explanation:

The function will be zero when the numerator is equal to 0. So, set the numerator equal to 0 and solve:

`0 = 4 {x}^(2) - 36x`

I will use the quadratic formula:

`\frac{ 36 + \sqrt{ {36}^(2) - 4(4)(0)} }{2(4)} \\ ( 36 + 36)/(8) = 9`

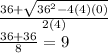
Therefore, x = 9 is a 0. Let's check with subtracted root now:

`\frac{ 36 - \sqrt{ {36}^(2) - 4(4)(0)} }{2(4)} \\ ( 36 - 36)/(8) = 0`

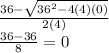
It appears 0 is also a root.

Therefore, the answer is D.