Question

use the intermediate value theorem to determine whether the following equation has a solution or not x^3-3x-1

Answer 1

Yes, this equation has a solution. According to Intermediate Value Theorem at least one solution for [0,2]

Explanation:

Hi there!

1) Remember a definition.

Intermediate Value Theorem:

If
`f` is continuous on a given closed interval [a,b], and f(a)≠f(b) and f(a)<k<f(b) then there has to be at least one number 'c' between 'a' and 'b', such that f(c)=k

----

(Check the first graph as an example)

2) The Intermediate Value Theorem can be applied to determine whether there is a solution on a given interval.

Let's choose the interval
`[0,2]`

`f(x)=x^(3)-3x-1\\f(0)=(0)^(3)-3(0)-1\\f(0)=-1\\f(0)<0\\`

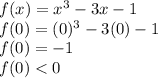
Proceed to the other point: 2

`f(x)=x^(3)-3x-1\\f(2)=(2)^(3)-3(2)-1\\f(2)=1\\f(2)>0\\`

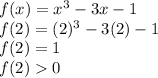
3) Check the 2nd Graph for a the Visual answer, of it. And the 3rd graph for all solutions of this equation.