Question

An observer stands on the side of the front of a stationary train. When the train starts moving with constant acceleration, the observer manages to measure the time it.takes for the second cart to pass him to be 5.0 seconds How long will it take for the 10th car to pass him? Assume all cars to be of the same length.

a. 2.8 s
b. 2.4 s
c. 2.0 s
d. 1.5 s
e. 1.1 s

Answer 1

To solve this problem we will use the linear motion description kinematic equations. We will proceed to analyze the general case by which the analysis is taken for the second car and the tenth. So we have to:

`x = v_0 t (1)/(2) at^2`

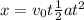
Where,

x= Displacement

`v_0` = Initial velocity

a = Acceleration

t = time

Since there is no initial velocity, the same equation can be transformed in terms of length and time as:

`L = (1)/(2) a t_1 ^2`

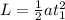
For the second cart

`2L (1)/(2) at_2^2`

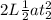
When the tenth car is aligned the length will be 9 times the initial therefore:

`9L = (1)/(2) at_3^2`

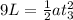
When the tenth car has passed the length will be 10 times the initial therefore:

`10L = (1)/(2)at_4^2`

The difference in time taken from the second car to pass it is 5 seconds, therefore:

`t_2-t_1 = 5s`

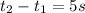
From the first equation replacing it in the second one we will have that the relationship of the two times is equivalent to:

`(1)/(2) = ((t_1)/(t_2))^2`

`t_1 = (t_2)/(√(2))`

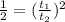
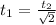
From the relationship when the car has passed and the time difference we will have to:

`(t_2-(t_2)/(√(2))) = 5`

`t_2 (√(2)-1) = 3√(2)`

`t_2= ((5√(2))/(√(2)-1))^2`

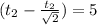
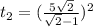
Replacing the value found in the equation given for the second car equation we have to:

`(L)/(a) = (1)/(4) ((5√(2))/(√(2)-1))^2`

Finally we will have the time when the cars are aligned is

`18 (1)/(4) ((5√(2))/(√(2)-1))^2 = t_3^2`

`t_3 = 36.213s`

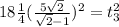
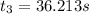
The time when you have passed it would be:

`20(1)/(4) ((5√(2))/(√(2)-1))^2 = t_4^2`

`t_4 = 38.172`

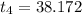
The difference between the two times would be:

`t_4-t_3 = 38.172-36.213 \approx 2s`

Therefore the correct answer is C.