Option B
12 over quantity x minus 7, x ≠ 7, x ≠ −3
Solution:
Given that we have to simplify quantity 12 x plus 36 over quantity x squared minus 4 x minus 21
So we have to simplify,
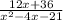
We have to find the restrictions on the variable
The above given Rational function is defined, for
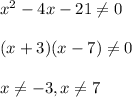
In order to simplify the above expression, we need to factor both the numerator and the denominator
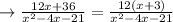
For the denominator, we need to split the middle term of the quadratic to get factored form,
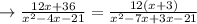
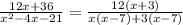
Fcatoring the denominator part,
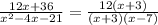
Cancel out common factors to get,
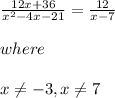
Thus option B is correct. 12 over quantity x minus 7, x ≠ 7, x ≠ −3